Bài 2: Yoni Đơn vị - Mối tương quan kích thước và phương pháp vẽ Mandala đồng tâm.

Bài 2: Yoni Đơn vị - Mối tương quan kích thước và phương pháp vẽ Mandala đồng tâm.

(Jaya Thiên) 

Trong bài trước, chúng tôi đã giới thiệu về “Khảo sát Mối Tương Quan giữa cạnh Yoni với cạnh trong Tháp Champa”, bằng phương pháp hình học dây để xác định được các đường tròn đồng tâm và các hình vuông nội-ngoại tiếp nó như một cách thực hành vẽ một mandala biểu tượng. Xem Yoni là đơn vị hạt nhân, ta chọn kích thước cạnh Yoni như một đơn vị kích thước hạt nhân ban đầu thể thực hành phép tính này. Kết quả thu được theo tỉ lệ (Cạnh Yoni : Cạnh trong tháp) được biểu diễn như sau:

• Mỹ Sơn A1, Pode Nagar Nha Trang, MS C1, MS E4, MS F1, MS A, Phố Hài : Cạnh Yoni = Cạnh hình vuông nội tiếp thứ 4 = 1/√2 x1/√2x1/√2x1/√2 =1/4 Cạnh lớn trong.

• MS C3, MS E5 , MS G1, Yang Mum , MS B4 , MS A10: Cạnh Yoni = Cạnh hình vuông nội tiếp thứ 3 = 1/√2x1/√2x1/√2 =1/2x 1/√2 Cạnh lớn trong.

• MS E1, MS C7: Cạnh Yoni = Cạnh hình vuông nội tiếp thứ 5 = 1/√2x1/√2x1/√2x1/√2x1/√2 =1/4x1/√2 Cạnh lớn trong.

Trong bài này, chúng tôi chọn điển hình Kalan Chính của Đền-Tháp Po klong Garai (ứng với tỉ lệ Cạnh yoni = 1/4 cạnh trong tường tháp) để diễn giải phương pháp vẽ các Mandala đồng tâm và tỉ lệ hình học được áp dụng để tính toán. (Xem các hình tham khảo đính kèm)

Như đã xác nhận, Yoni chính là giá trị kích thước ban đầu là một đơn vị. Theo thứ tự lần lượt, chúng tôi dùng phương pháp tách lớp để cố gắng trình bày một cách dễ hiểu nhất và có thể tự thực hành.

• Bước 1: Chọn bệ Yoni có dạng hình vuông với cạnh AxA (Với A=2a), ta thu được được hình vuông cạnh (a x a) được phân chia bởi hai đường trục Đông-Tây, Nam-Bắc.

• Bước 2: Thực hiện phép vẽ hình chữ nhật tỉ lệ vàng từ hình vuông cơ sở có cạnh (a x a) thu được từ bước 1, với tâm điểm gốc O, thực hiện phép vẽ hình chữ nhật tỉ lệ vàng (tỉ lệ vàng trong toán học và nghệ thuật) với tỉ lệ đoạn thẳng: (O1)/(12)=(O2)/(O1) = 1.618 = Phi (φ), tương ứng với mỗi lớp đường tròn khai căn (√1, √2, √3,…) lần lượt ta thu được các hình chữ nhật tỉ lệ vàng tương ứng, đồng thời ta vẽ được các đường tròn Mandala đồng tâm với điểm gốc Tâm O như hình tương ứng. Kết quả thực hiện từ phép vẽ này đến hình chữ nhật √8, đồng thời ta thu được đường tròn Mandala lớp 8. Chính Mandala lớp 8 này là điểm giới hạn không gian trong lòng tháp (Cạnh tường trong Tháp). Cũng bằng phương pháp này ta tìm được Cạnh tường ngoài Tháp và Chân đế tường ngoài Tháp.

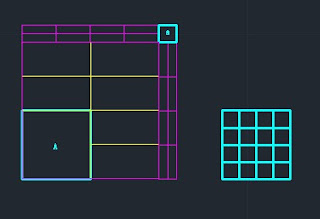
• Bước 3: Kết quả thu được tại bước 2 được biểu diễn như hình minh hoạ. Với hình vuông cơ sở ban đầu có cạnh (a x a) ta thu thêm được 3 hình vuông có cùng kích thước với hình vuông cạnh (a x a) ban đầu, và nó đúng bằng kích thước của một hình vuông Yoni có cạnh (A x A). Hay có thể nói, từ Yoni ban đầu ta tìm được điểm giới hạn không gian cạnh tường trong của Tháp với phép duỗi thẳng 4 ô vuông từ phép chia ở bước 1.

• Bước 4: Ta biểu diễn kết quả thu được ở bước 2 bằng hình vuông cân bậc hai tại lần thứ 8 (√8), Kết quả thu được ta tìm được: hình vuông (a) = 1/16 hình vuông (A). Mà hình vuông (A) chính là hình vuông ¼ yoni được chọn ở bước 1.

• Bước 5: Kết quả thu từ bước 4 ta đem vào đồ hình mặt bằng tháp, kết quả thu được lần lượt tương ứng với: 64 ô vuông (a) được tạo bởi hệ ô lưới (8x8) cho hình vuông Yoni; 1024 ô vuông (a) được tạo thành bởi hệ ô lưới (32x32) cho hình vuông cạnh trong Tháp; 4096 ô vuông (a) với hệ lưới (64x64) cho hình vuông cạnh ngoài Tháp; 5184 ô vuông (a) với hệ lưới (72x72) cho hình vuông cạnh chân tường ngoài Tháp.

Các kết quả thu được từ phép vẽ trên cho chúng ta thấy được mặt bằng đồ hình Mandala của Đền Tháp Champa được tạo nên bởi tỉ lệ hoàn hảo mà ngày nay chúng ta biết được với tên gọi Tỉ Lệ Vàng. Nó được biểu diễn như hình đính kèm dưới đây. Với hệ số tỉ lệ AC/CB = AB/AC = AB/BD = AD/AB = 1.618 = Phi (φ)